Chip Select
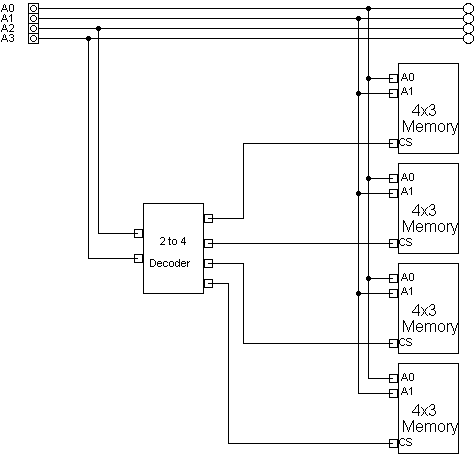
Consider a system that has four of the 4x3 memory chips we discussed in class.
-
Each chip only needs two address lines, since there are only four words
in each chip. Inside each chip, the addresses would be:
00, 01, 10, 11.
-
The number of words for the entire system is 16: 4 in each chip. How do the
chips know when a word is for them? The addresses for the entire system
are:
| 0000 |
0001 |
0010 |
0011 |
| 0100 |
0101 |
0110 |
0111 |
| 1000 |
1001 |
1010 |
1011 |
| 1100 |
1101 |
1110 |
1111 |
-
We will design the system so that the each row of addresses will correspond
to a different memory chip. The row addresses can be viewed as 00XX, 01XX,
10XX, 11XX. The X's represent the address inside the chip, the other two
bits are used to select one of the chips. Using a 2-to-4 decoder, the high
two address lines can be used to select the appropriate chip, the low two
address lines go to each memory chip.
A more complicated example
The example in the book in section 3.7.2 also shows how to configure chip
select for a larger address space, using different size chips.
-
The first step is to do address line calculations
-
The address space is 64K.
64K = 64 * 1K = 64 * 2^10 = 2^6 * 2^10 = 2^16
16 address lines are needed to access all of the 64K addresses.
-
Next is to determine how many of these address lines are needed for the chip.
Consider the EPROM. It is 2k in size.
2K = 2 * 1K = 2^1 * 2^10 = 2^11
11 address lines are needed to address all the addresses inside the EPROM.
-
A similar calculation reveals that the 2K RAM also needs 11 address lines.
-
The PIO chip only has 4 bytes inside, so it only needs 2 address lines.
-
The second step is do starting location calculations. The idea behind placing
the chips is to place them at multiples of there size. This keeps the circuitry
at a minimum (and the math). Therefore, a chip of size 2K will only be placed
at 0K, 2K, 4K, 6K, 8K, etc.
-
Consider the EPROM
-
Calculate how many multiples of the chip size there are in the address space.
64K/2K = 32
There are 32 possible multiples.
32 = 2^5
There will be 5 bits for the chip select lines.
-
Calculate which multiple corresponds to the starting location. For the EPROM,
the starting location is 0K.
0K / 2K = 0
Write the multiple as a binary number, using 5 places (one for each chip
select line).
00000
-
For the EPROM, the 16 bit address can be broken into 5 chip select lines,
and 11 lines for inside the EPROM
00000XXXXXXXXXXX
-
Consider the RAM
-
It is the same size as the EPROM, so it will also have 5 chip select lines.
-
Calculate the multiple that corresponds to 32K (the starting location for
the RAM)
32K/2K = 16
Write 16 as a binary number in 5 places.
10000
-
For the RAM, the 16 bit address can be broken into 5 chip select lines, and
11 lines for inside the RAM
10000XXXXXXXXXXX
-
Consider the PIO.
-
Calculate how many multiples of the chip size there are in the address space.
64K/4 = 16K
There are 16K possible multiples.
16K = 2^4 * 2^10 = 2^14
There will be 14 bits for the chip select lines to the PIO.
-
Calculate the multiple that corresponds to the last 4 bytes before 64K (the
starting location for the PIO). Theoretically, the PIO could be placed at
any multiple of 4. To keep the math simple, we will place the PIO either
at the start, or at the end of a 1K block in the address space.
A 1K block has 10 address lines. The PIO only needs 2 of those address lines.
The remainder are for chip select.
If the PIO is placed at the start of the 1K block, there would be 8 chip
select lines and 2 address lines as
follows:
00000000XX
If the PIO is placed at the end of the 1K block, there would be 8 chip select
lines and 2 address lines as follows:
11111111XX
This example places the PIO at the end of the 63K block.
64K/1K = 64
There are 64 possible multiples of 1K.
63K/1K = 63
Write 63 as a binary number in 6
places.
111111
Combining the 8 chip select lines with these 6, results in the
following
11111111111111XX
(If this chip were placed at the start of the 63K block, its chip select
lines would be
1111100000000XX)
Chips of different sizes
The same calculations work for chips of different sizes as well. Consider
a second EPROM of size 4K that starts at 40K. The EPROM now requires 12 address
lines for inside the chip.
-
Calculate how many multiples of the chip size there are in the address space.
64K/4K = 16
There are 16 possible multiples.
16 = 2^4
There will be 4 bits for the chip select lines.
-
Calculate which multiple corresponds to the starting location. For the EPROM,
the starting location is 40K.
40K / 4K = 10
Write the multiple as a binary number, using 4 places (one for each chip
select line).
1010
-
For the EPROM, the 16 bit address can be broken into 4 chip select lines,
and 12 lines for inside the EPROM
1010XXXXXXXXXXX

